円の接線の性質 証明 257088-円の接線の性質 証明

 「円の接線は、接点を通る半径に垂直である。 」 これを方冪（ほうべき）の定理（円の接線の性質）と言います。 中学生の段階では、他の定理と同じ様に、 「こういう事が成り立つんだ」と理解していれば良いと思います。 証明しようとすると、 数学IAIIB 数学ⅡB円周上の点における接線神奈川工科大・立教大・法政大 数学IAIIB 差をつける自宅学習を始めよう ここでは円周上の点における接線の方程式について説明します。 円の接線の方程式の公式を丸暗記することも重要ですが 円の接線の公式について 円の接線の方程式、あなたはすぐに求められますか？ 円の接線に関しては大変便利な公式があるのですが、これをしっかり覚えている受験生は意外と多くないんですよね。 公式を覚えていなくても求められなくはないのですが、計算の手間が何倍にも増えてしま

方べきの定理とは 証明や逆 応用問題をわかりやすく解説 受験辞典

円の接線の性質 証明

円の接線の性質 証明-円の性質のまとめ ここで4点が同一円周上のあるための条件，直線が円の接線になるための条件に注目して 円の性質をまとめておきます． なお，証明は，最後のトレミーの定理以外，すでに学んだページを参考にして下さい． 命題 四角形abcdで次が成り立つ．弧に対する円周角の性質 の意味を理解している。 ②円周角と中心角の関係 が証明できることを理解 している。 ③円周角の定理の逆の意 味を理解している。 ④円の外側にある1点か ら円に接線をひく作図の 方法や、長方形を使って 円の中心を求める方法な

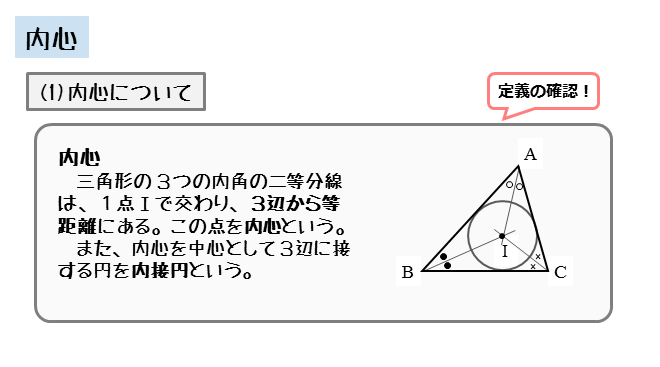
図形の性質 内心について 日々是鍛錬 ひびこれたんれん

円外の点から引いた接線 図形と方程式 (教科書範囲) ★★ 円の外部の点から引いた接線を扱います． 円の接線の公式 が既習である前提です． 解法が複数あるので，ここで整理します． 目次 1： 円外の点から引いた接線の求め方 2： 例題と練習問題二等辺三角形の図形的性質は大丈夫ですね？ 左右対称です。 接線と半径は垂直 半径（正しくは円の中心と接点を結んだ線分）と、その点における接線は垂直 例題1 半径が \(11cm\) の円 \(O\) で、中心との距離が \(5cm\) である弦 \(AB\) の長さを求めなさい。 解答ポイント 円の接線の方程式の証明方法 Ⅰ 傾きを求める方法 Ⅱ 接点を通る直線を設定し，円と連立して接点で重解になることから導く方法 Ⅲ 点と直線の距離を使う方法 Ⅳ 法線ベクトルを使う方法 Ⅴ (数学Ⅲの)微分を使う方法 こうしてみると手段が

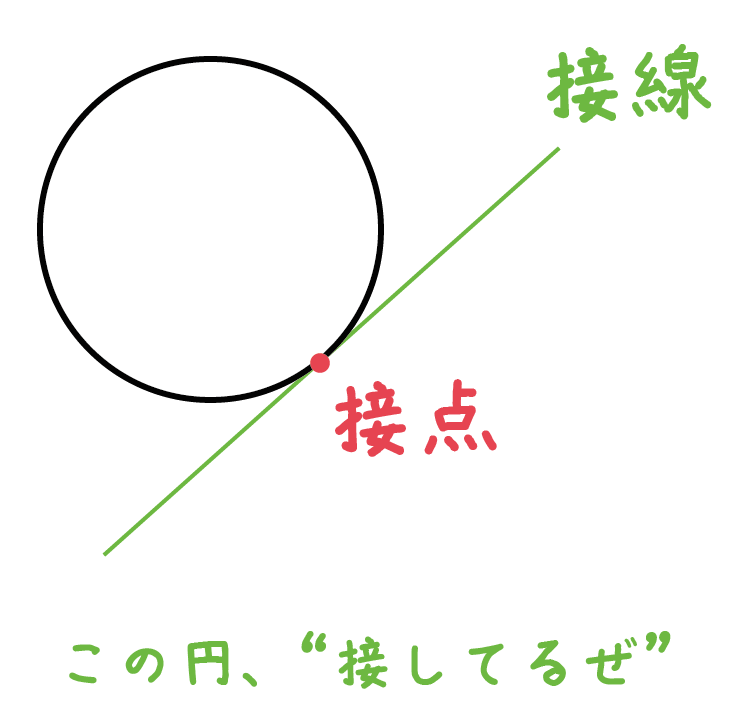
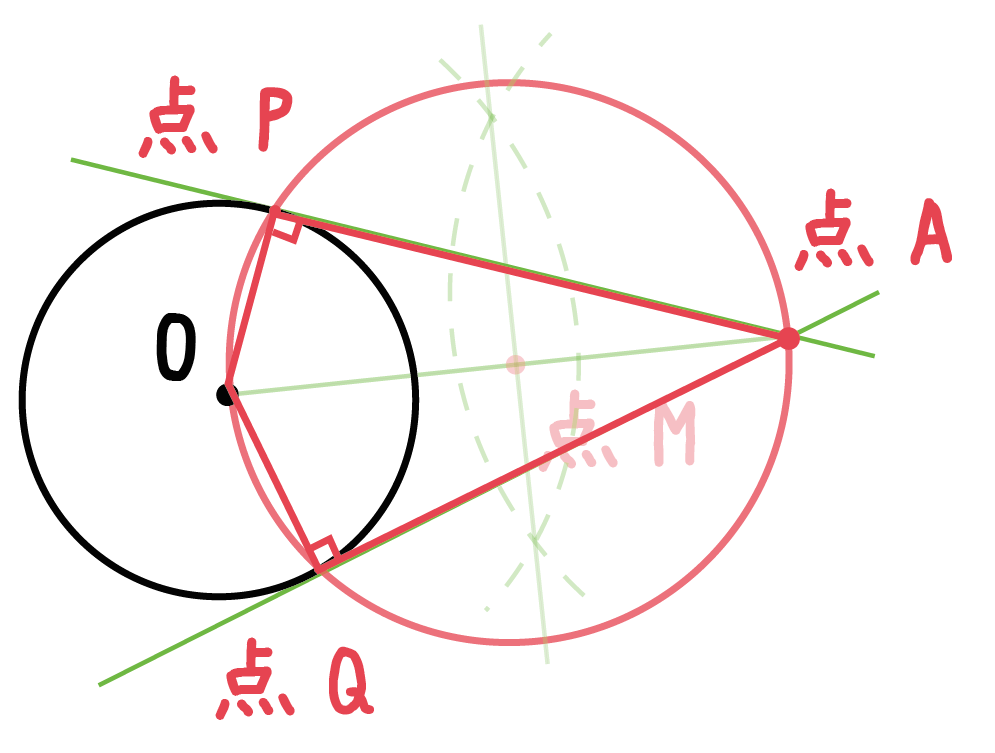
「円の接線は、接点を通る半径に垂直」になる説明 まずは、下の図のように円と2点で交わる直線を引いて、円と直線の交点を点A、点Bとします。 円の中心を点O、 直線ABの中点を点M とします。 ここで、三角形AMOと三角形BMOは、3辺の長さが全て同じなので、合同な三角形になっています。数学a 第3章 図形の性質 証明の流れ 1．点aを通る接線上に点t$'$をとる． 従って2直線at，at'は一致するから，直線atは円の接線である． 円周角の定理の極限 次に，接弦定理が成り立つことの感覚的な説明を紹介します。 点 c c c を円周上で限りなく a a a に近づけていくと， 円周角の定理より ∠ a c b \angle acb ∠ a cb は一定 直線 c a ca c a は円の接線に近づく 以上から接弦定理が成り立つことが納得できます。

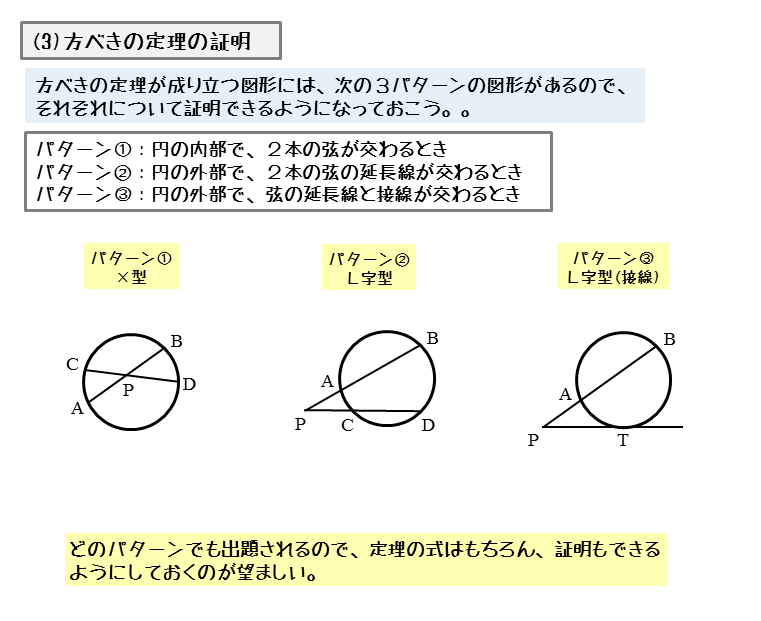
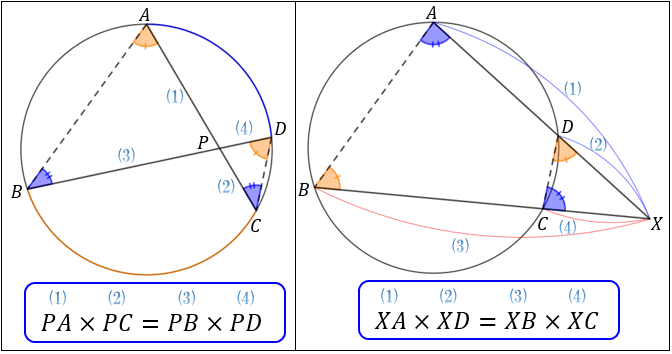
方 べきの 定理とは， 平行でない 2 本の直線と円とが交わって（接して）できる図形の辺の長さの関係 を示している公式です。基本的には 3 つの形があります。 どれも三角形の相似から証明することができます。 ① 2 つの直線の交点が円の内部にあるとき このとき， が成り立ちます。 原点を中心とする円の接線の方程式 円 x2 y2 = r2 x 2 y 2 = r 2 に接する直線、つまり、接線の方程式について考えましょう。 接線は何本でも引けますが、接点を決めれば接線は1本に決まります。 ここでは、接点を (x1,y1) ( x 1, y 1) としましょう。 これは円放物線の基本定理 作成者 Bunryu Kamimura トピック 放物線, 三角形 放物線とその準線には面白い性質がある。 そこで、放物線に外接する三角形を作図してみる。 すると、この三角形の心と焦点や極との間に面白い性質が見つかってくる。 それらの発見を

数学a 平面図形 円の性質 ２つの円の共通接線

接弦定理とは何か 角度別に分かるその証明方法 アタリマエ

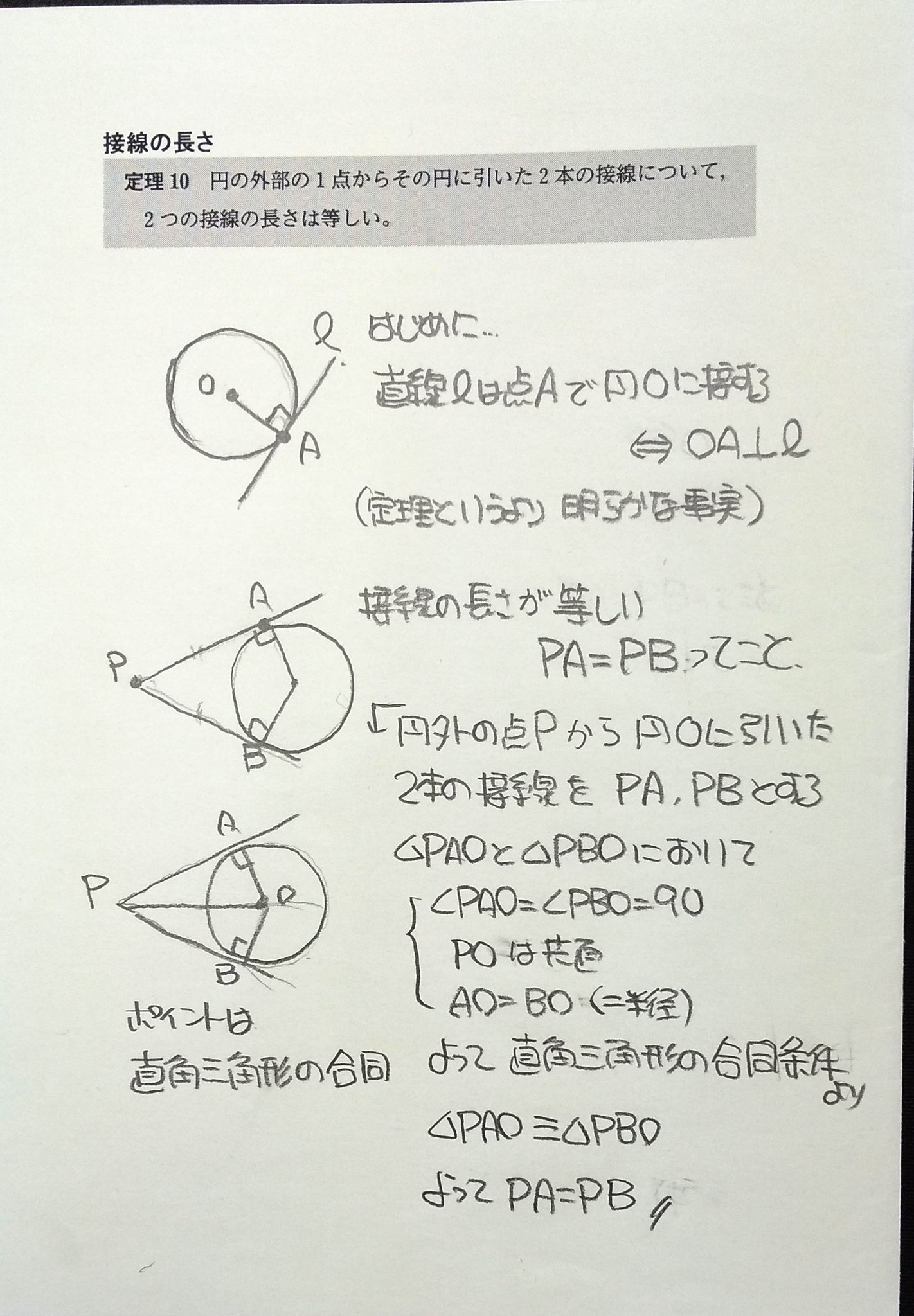
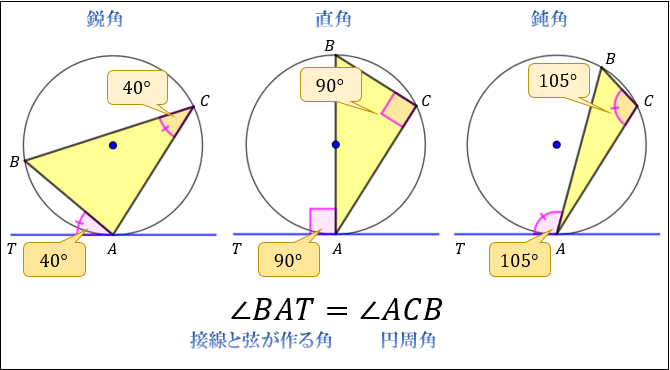
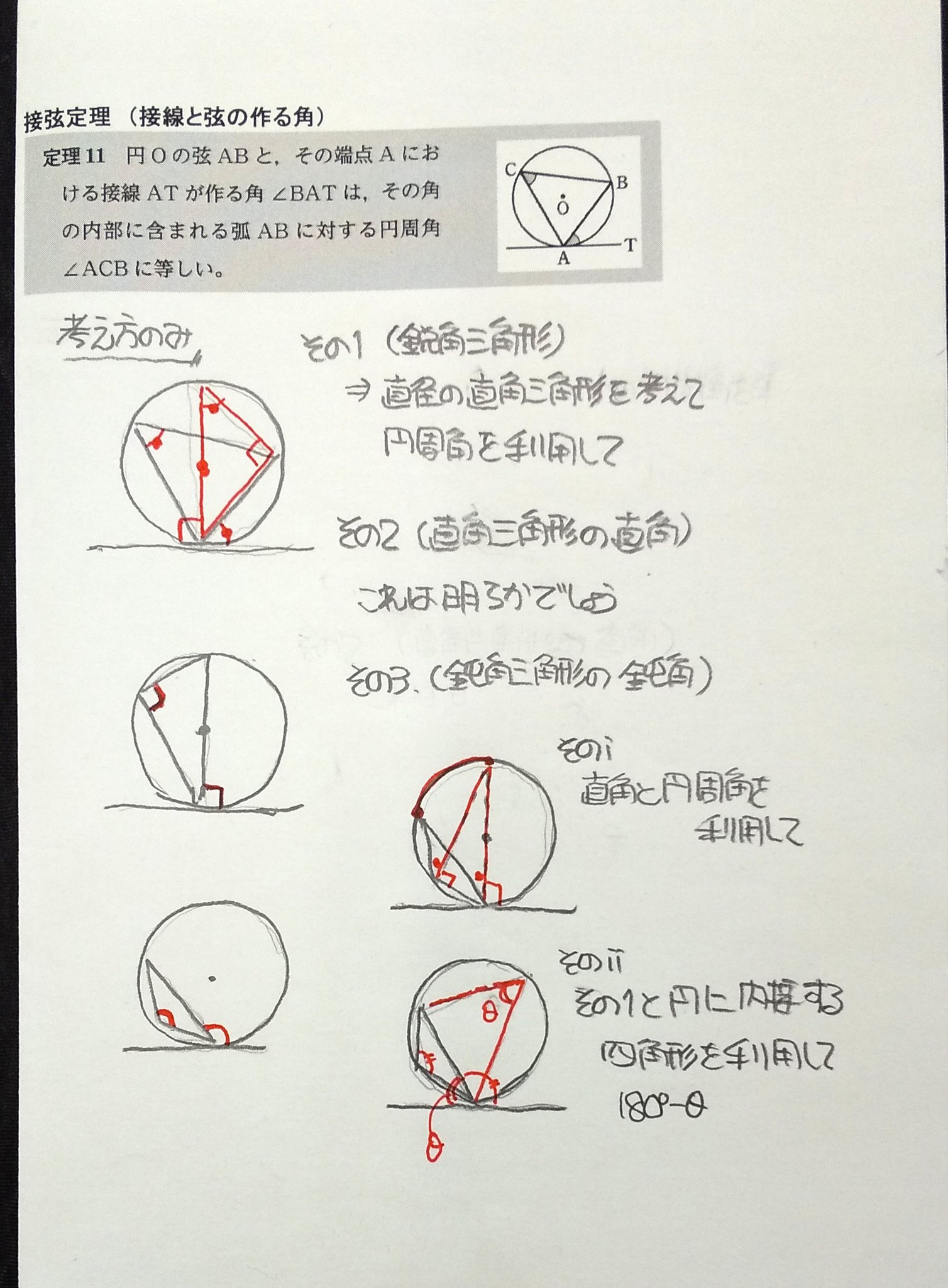
円の接線は接点を通る半径に垂直である。 証明 円Oの直径ABをとる。 点Bを通る接線と、点Aと円周上の点Cを結んで延長した線の交点をDとする。 ABDと BCDにおいて、 円の接線とその接点を通る弦の作る角は、その角の内部にある孤に対する円周角に 角度別に分かるその証明方法 「円の接線 A T と弦 A B が作る角 ∠ B A T は、弦 A B に対する円周角 ∠ A C B と等しい」という定理を、 接弦定理 と言います。 接弦定理は、 ∠ B A T が鋭角・直角・鈍角のどの場合でも成り立ちますが、それぞれ証明の仕方が 要点 円の接線の性質 円の接線は、その接点を通る半径に垂直である。 円の外部の点からその円にひいた2本の接線の長さは等しい 直角三角形の合同の証明を利用して 円の接線の性質を利用して辺の長さを求める

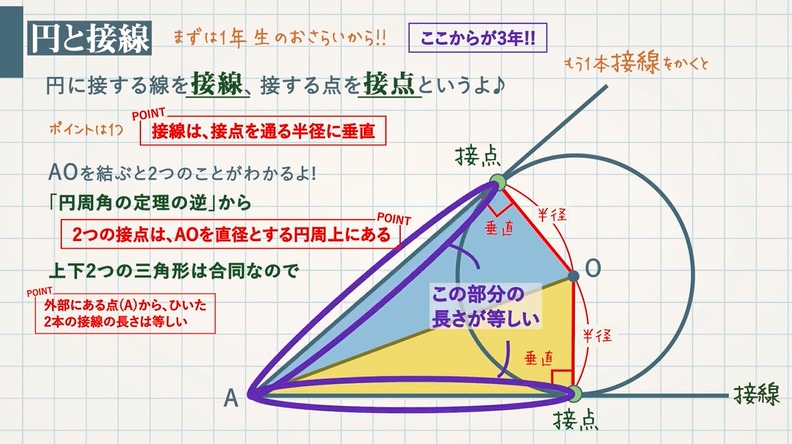
円と接線 教遊者

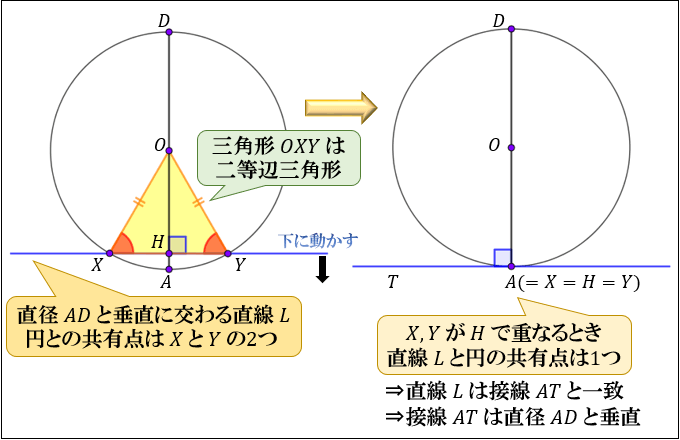
接弦定理とは何か 角度別に分かるその証明方法 アタリマエ

接線と弦のつくる角の定理の証明 では、なぜこのような定理が成り立つのか。 簡単に確認しておきましょう！ なぜ、次のような位置にある角の大きさが等しくなるのでしょうか。 これを考えるには、まず 接点から、直径になるように線を引いて 下の (1) aから円には2つの接線が引ける。それらの接点をそれぞれb,cとする。直線bcの方程式を求めよ。 (2) 直線bc上かつ円の外側に点dをとる。dから円には2つの接線がひける。それらの接点をe,fとする。このとき点aは直線ef上にあることを証明せよ。円の接線に関しては，以下の2つのことが成り立ちます。 1． 円 の接線 は，接点 を通る半径 に垂直になる。 2． 円 の周上の点 を通る直線 が半径 に垂直ならば， はこの円の接線になる。 そしてこの2つのことから接線の長さに関して， 円の外にある 1

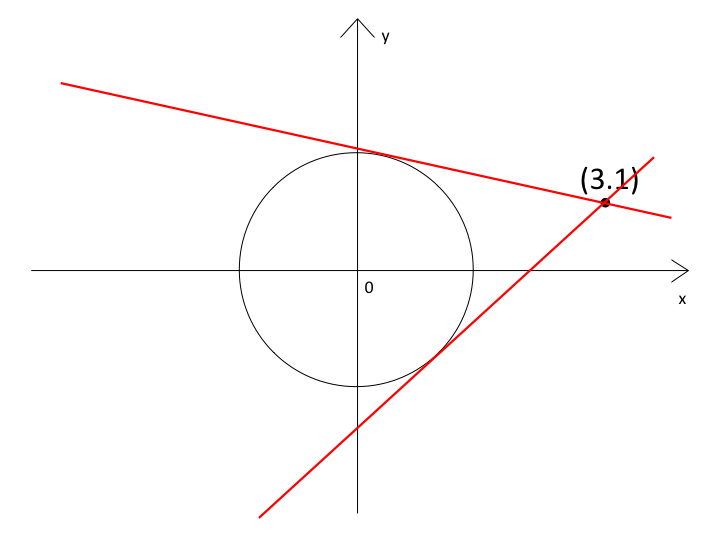
3分で分かる 円の接線を求める公式とその使い方をわかりやすく 合格サプリ

円の接線の長さの証明 数学a By となりがトトロ マナペディア

5図形の性質と証明 円の接線を作図しよう 10 2 年 組 氏名 1 古代ギリシアの数学者ユークリッドは，いくつかの基本的な図形の性質をもとにして， 様々な図形の性質を証明し，有名な「原論」にまとめました。 この原論の第3巻に，「与えられた点から与えられた円に接線をひく」作図の方法が紹介 関連記事 図形の性質｜内心について また、 接弦定理 とは、 接点を通る弦と接線とがつくる角は、その角の内部にある弧に対する円周角と等しくなる という定理です。 その角の内部にある弧とは、弦によって円周が2つの弧に分けられたときの、 弦と円に内接する四角形の角度 円に内接する四角形の対角の和は 180° である。 → a c = 180°, b d = 180° 円に内接する四角形の外角は，対角 (内角)に等しい。 → a の外角は c の角度と同じ。 証明 ここでは，a c = 180 を説明 (証明)します。 円 周 角 ： に 対

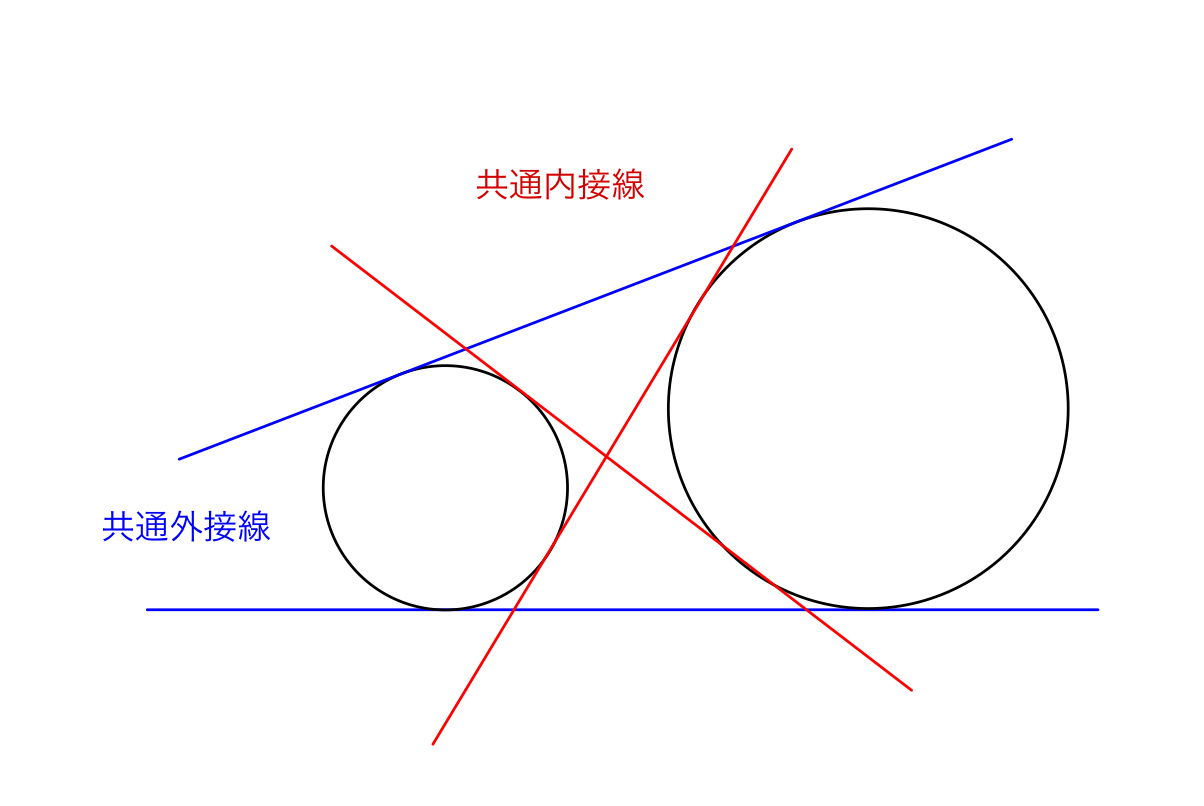
共通接線の問題5パターンの解き方を例題付きで解説 東大医学部生の相談室

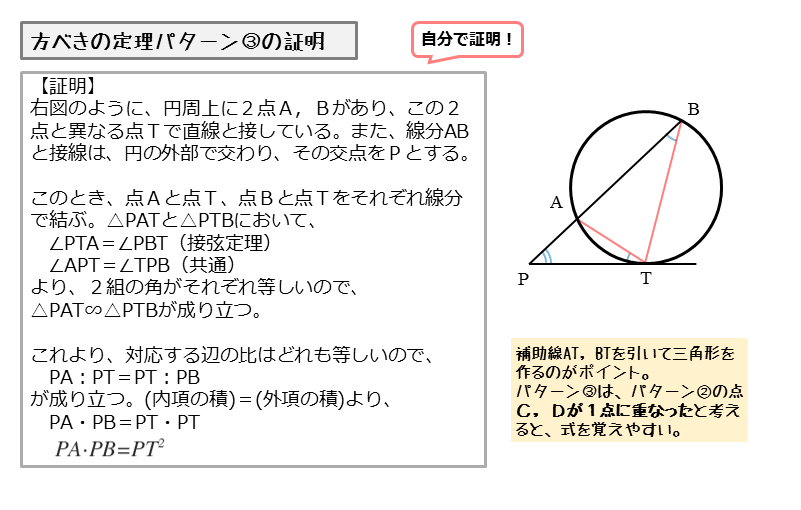
図形の性質 方べきの定理について 日々是鍛錬 ひびこれたんれん

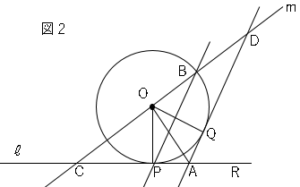
 さっきの「円の接線の性質」、 円の接線は、その接点を通る半径に垂直である をつかえば、 線分pa、qaは円の接線 ってことになるんだね。 これは中2数学でならう内容だから、今はまだわからなくても大丈夫だよー。 まとめ：円の接線の作図は2パターン 今回は円の接線の方程式・公式を扱います。 円の方程式・公式は、高校数学で必ず覚えなければいけないことの1つです。 今回は誰でもわかる丁寧な証明と、練習問題も掲載しています。 ぜひこの機会で円の接線の方程式・公式をマスターしましょう二つの円が交じり合うと、共通接線や弦ができます。 これを円同士が離れていても成り立つように拡張するにはどうしたらいいのでしょうか。 ジオジェブラの中にある極線を使うとできることに気がつきました。 この極線はとても大切な線です。

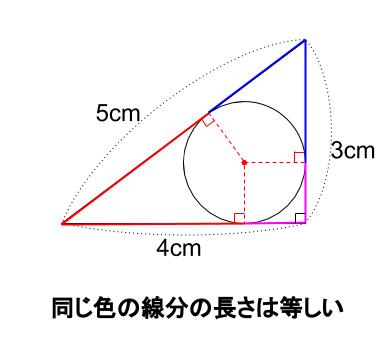
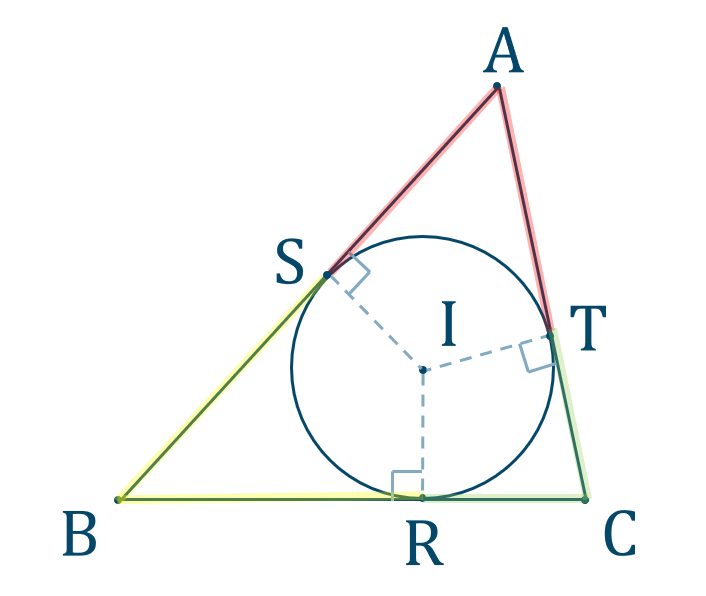
三角形の内接円 中学数学の無料オンライン学習サイトchu Su

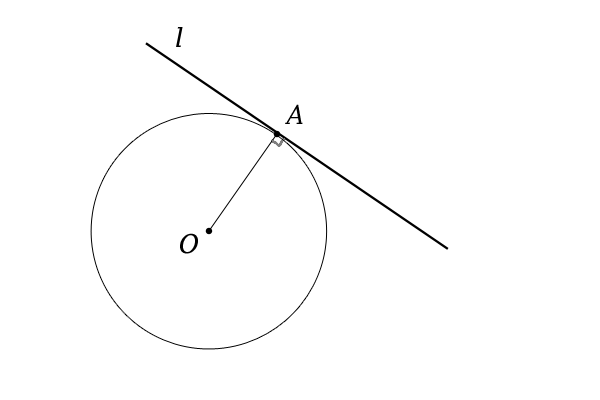
円と直線の距離と位置関係 特に交点 接点 接線について 高校数学マスター

この接線を考える場合には、2円に次のような特徴があることを覚えておきましょう。 先ほどの接線の作図を理解できれば、こちらも同じような考え方で進めていきます。 まずはそれぞれの中心を通るような円をかきます。 その後、半径 となるような円 数学円の接線の方程式の求め方（解法③：接点を求めて計算量を軽くしたい）高校 数学 図形と方程式 数学2（質問ありがとうございます！ 今回は、こんな質問をいただきました↓ 点（4, 6)を通り、円 (x －1)2 (y － 1)2 = 9 に接する直線の方程式は？証明 背理法を用いる。 点 O を中心とする円に直線 \ell が点 A で接しているとする。 また、直線 \ell に点 O から垂線を下ろし、交点を B とする。 このとき、 \ell と線分 OB が成す角 \angle B は90°である。 ここで、 \ell と直線 OA が成す角 \angle A が90°ではないと仮定する（背理法の仮定）。

図形の性質 内心について 日々是鍛錬 ひびこれたんれん

方べきの定理の証明 １本が円の接線の場合 数学a By となりがトトロ マナペディア

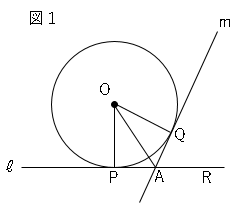
 円の接線と半径 あとで、円の接線を作図する方法を見るのですが、その前に、円の接線に関する重要な性質を見ておきます。 直線 $\ell$ が円 O と接しているとします。このとき、円の中心と接点 P とを結ぶと、この線分 OP は接線 $\ell$ と垂直に交わります。 中3 円の性質 カテゴリーの記事一覧 すべて無料！ 星組の中学数学講座 授業動画は声と手だけ、テキストは下手な字で手書きの低クオリティー！ だけど、内容は役に立つと思います。 また、無料学習プリント集としてもお使いいただけます。 ちなみに 円の接線 高校受験などでよく出てきますね、 そこで円の接線の基本から作図、応用的な作図まで紹介します！ 接線とは 接線の性質 円の外部の点を通る接線の作図 円の外部の点を通り円に外接する円の作図 (応用編)二つの円の共通接線の作図 (応用編)円の外部の二点を通り円に外接する円

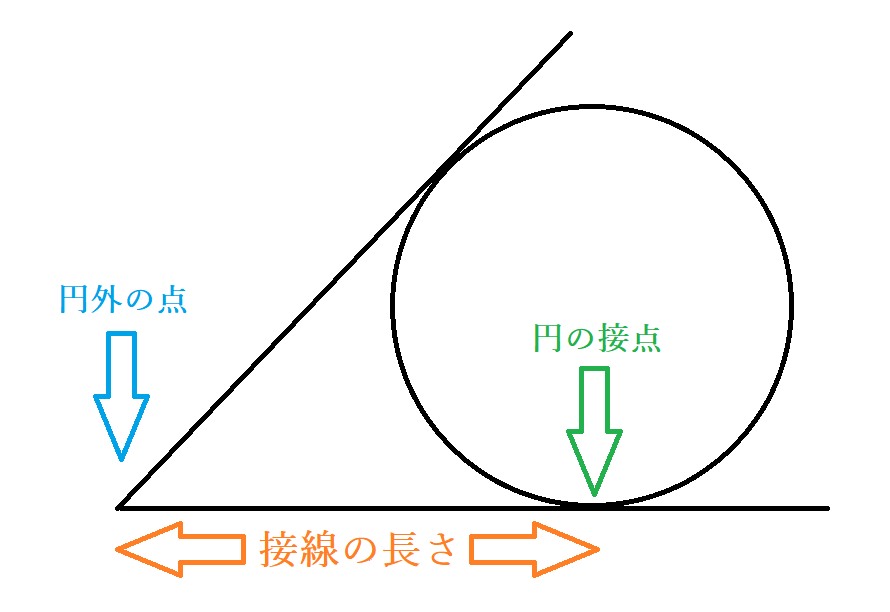
円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの学びblog

公式一覧と使い方 解き方 数学ａ 図形の性質 教科書より詳しい高校数学

 円の性質になります。円周角の定理、弧と円周角の関係、円と接線の関係を解説しています。 これらは主に 相似 を証明するときに使います。次の空欄に入る適当な語句を選んで，「接弦定理」の証明を完成させなさい． (証明) 円の接線と弦の作る角が(1)直角(90)，(2)鋭角(90 より小さい)，(3)鈍角(90 より大きい)の3つの場合に分けて示すこととします． (1) BAT＝90 のとき (漢字2文字を入れなさい↓) このように 「原点が中心の円」 で 「接点が ( x 1 − a, y 1 − b) である接線の方程式」 を考えることになります。 ここがミソです。 そうすると先ほど私たちが覚えた接線の公式が使えて ( x 1 − a) x ( y 1 − b) y = r 2 とできますね。 あとは 円を元の位置

中3数学 接線の長さ 練習編 映像授業のtry It トライイット

1

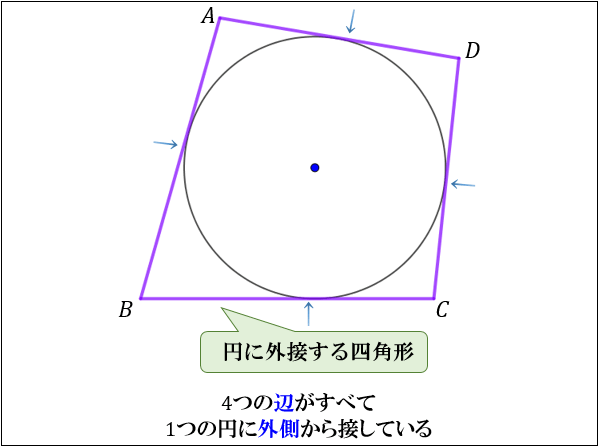
円に外接する四角形の性質まとめ 向かい合った辺の合計が等しくなる理由 アタリマエ

円の方程式の公式や求め方をわかりやすく解説 円の接線も 受験辞典

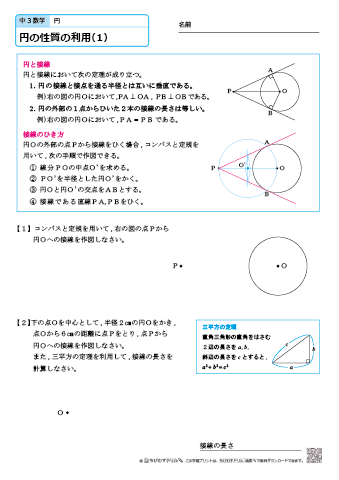
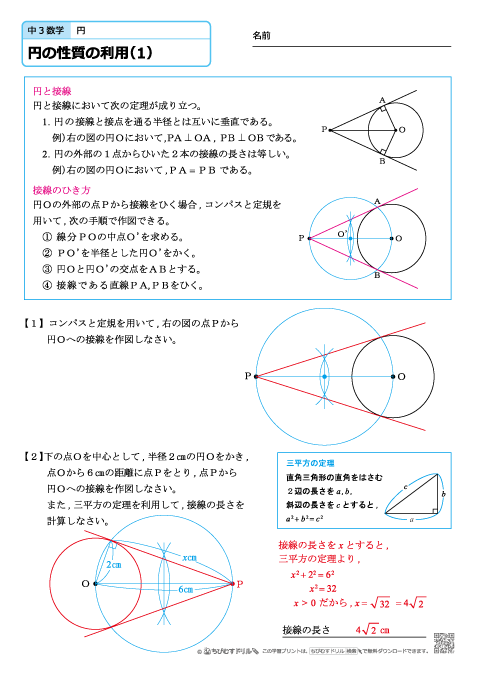
中学３年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生

中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく

接線の長さ 円の接線 一夜漬け高校数学586 数学a 図形の性質 Youtube

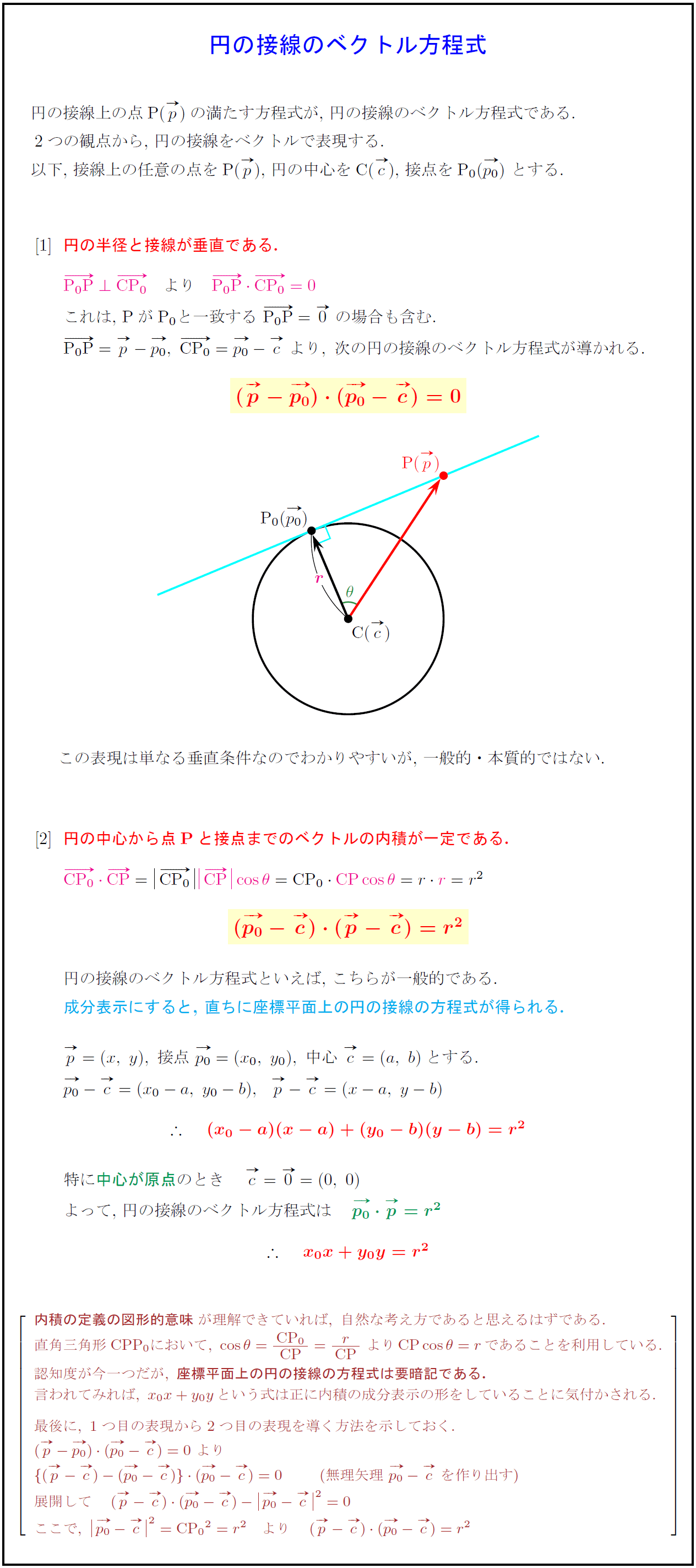
高校数学b 円の接線のベクトル方程式2パターン 受験の月

円の接線が半径に垂直であることの証明 Youtube

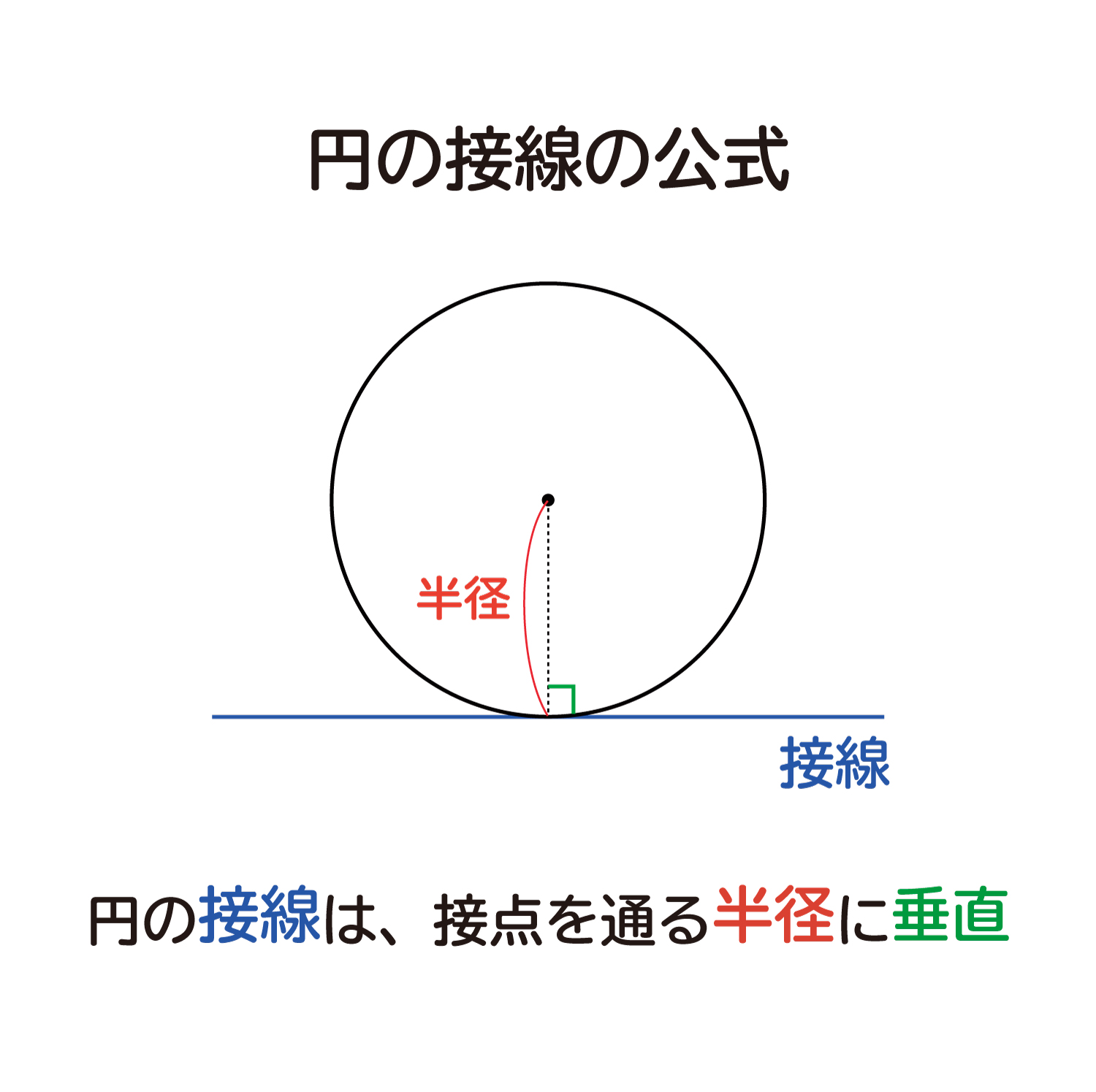
なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル

中3数学 円の性質15 円と接線 すべて無料 星組の中学数学講座

原田 浩明 Pa Twitter Sサクシード059 円の接線の長さ 接弦定理 接線と弦の作る角の定理 高校 数学 １年 数学a 図形の性質 定理の証明 T Co I1zkawby6b Twitter

三平方の定理の証明 内接円を利用した証明方法をわかりやすく解説 面積と接線の性質をフル活用 Fukusukeの数学めも

方べきの定理の証明 １本が円の接線の場合 数学a By となりがトトロ マナペディア

円の接線の方程式

接弦定理とは何か 角度別に分かるその証明方法 アタリマエ

数学ａの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア

図形の性質 方べきの定理について 日々是鍛錬 ひびこれたんれん

円の接線 数学a By Okボーイ マナペディア

方べきの定理とは 3つのパターンの図解とその証明方法 アタリマエ

接線についていろいろ 身勝手な主張

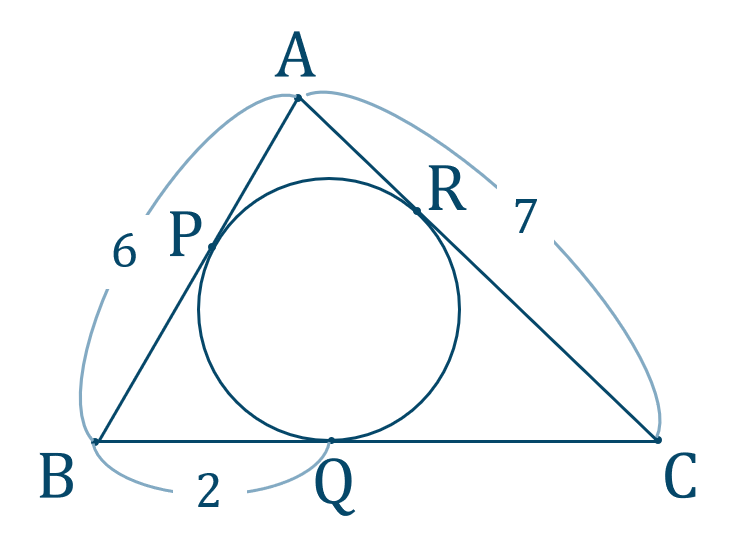
数学ａ 内接円と接線の条件の使い方とコツ 教科書より詳しい高校数学

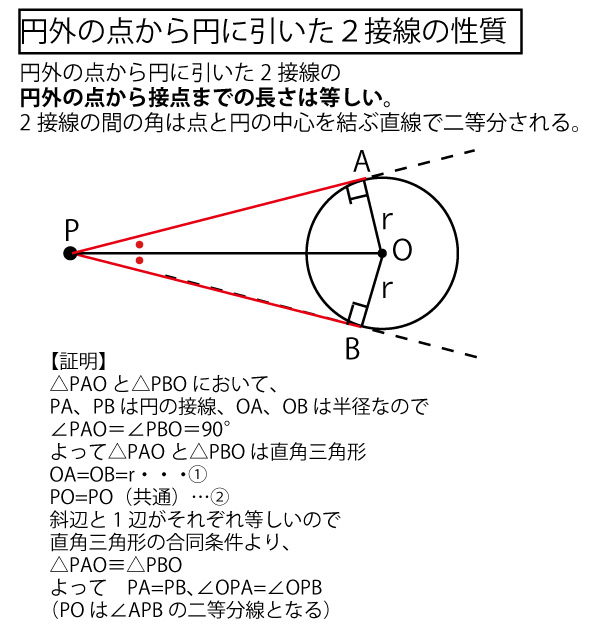
21年大学入試共通テスト 数学ia 第5問 選択 図形 配点点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

円の接線の方程式は一発で求めよう 公式を考え方から説明

中学数学 円と接線 Youtube

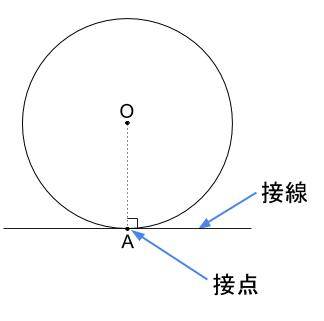
中学数学 三平方の定理 円と接線 弦 中学数学の無料オンライン学習サイトchu Su

1

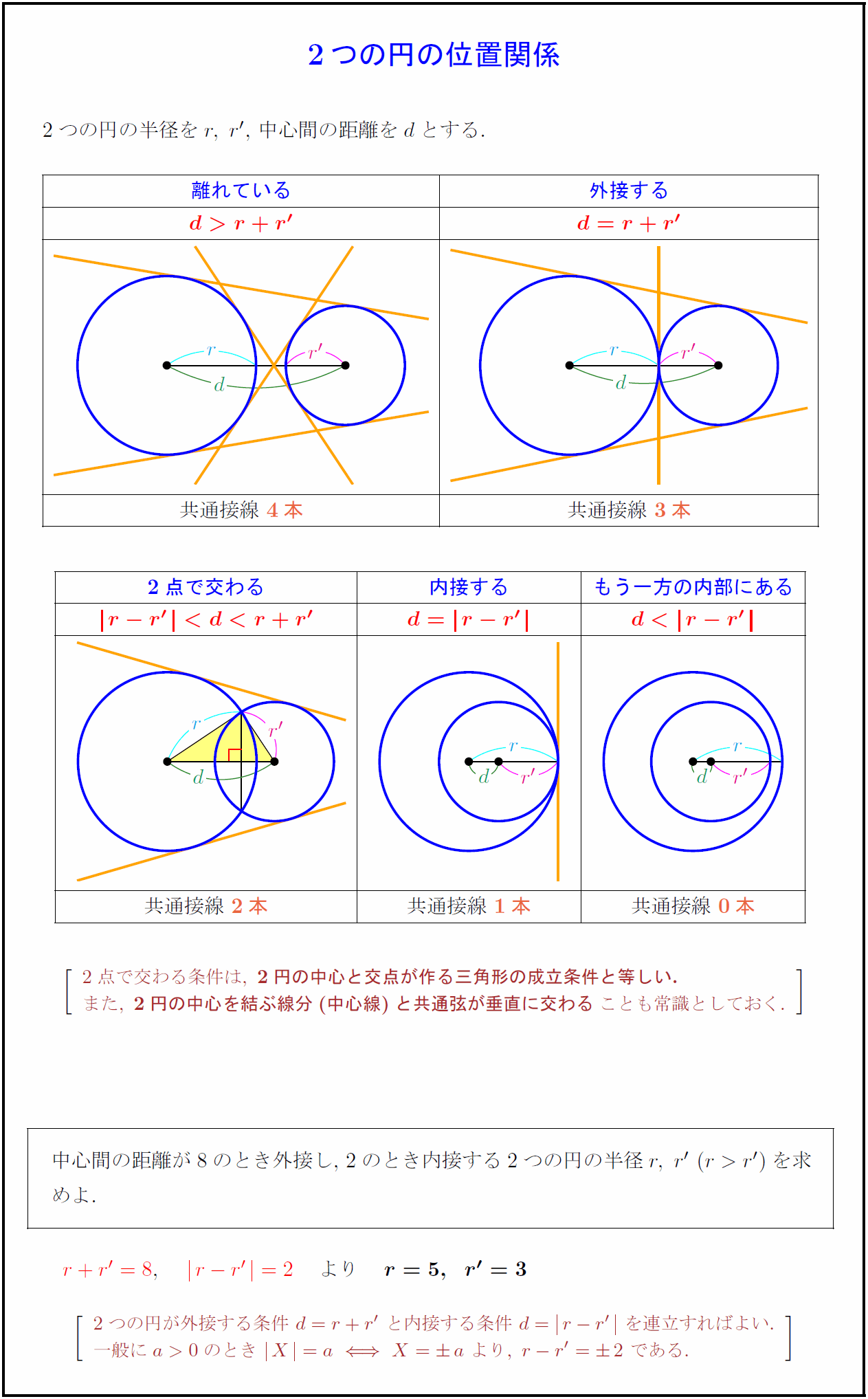
高校数学a 2つの円の位置関係5パターン 受験の月

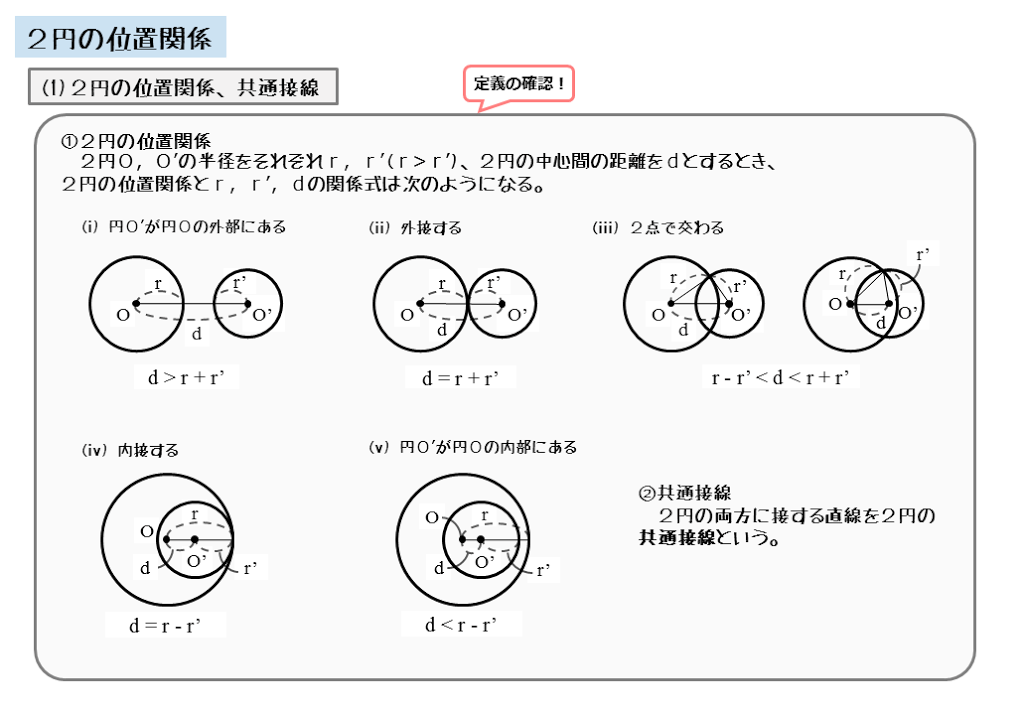
図形の性質 ２円の位置関係について 日々是鍛錬 ひびこれたんれん

標準 円の接線と作図 なかけんの数学ノート

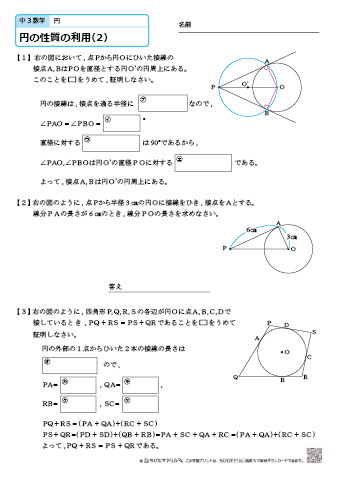
中学３年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生

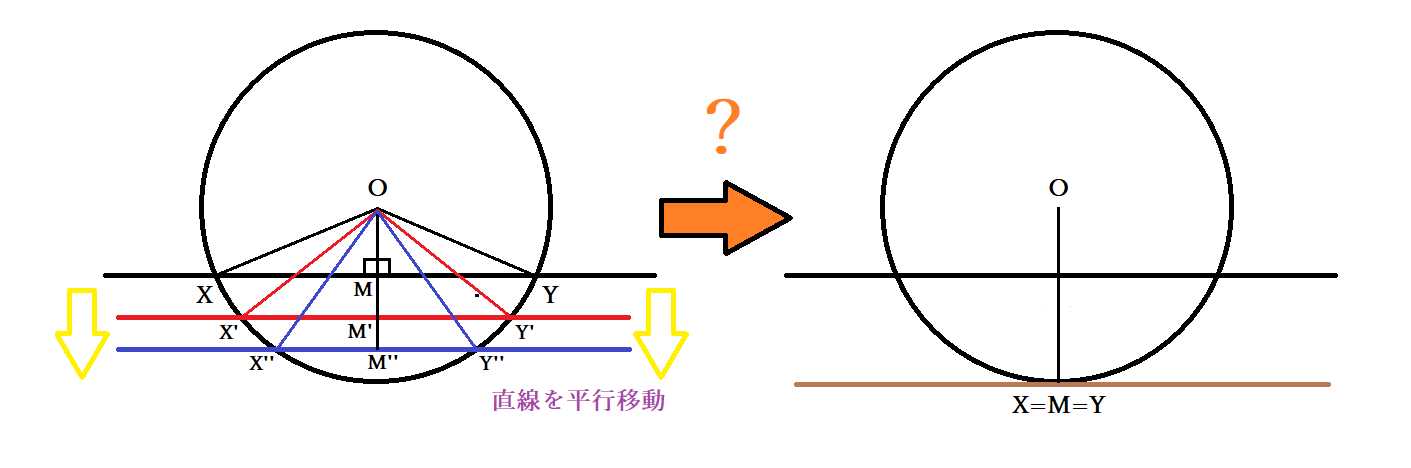
数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの学びblog

3

Tikz 高校数学 円の接線と弦のつくる角 接弦定理 の証明 数樂管理人のブログ

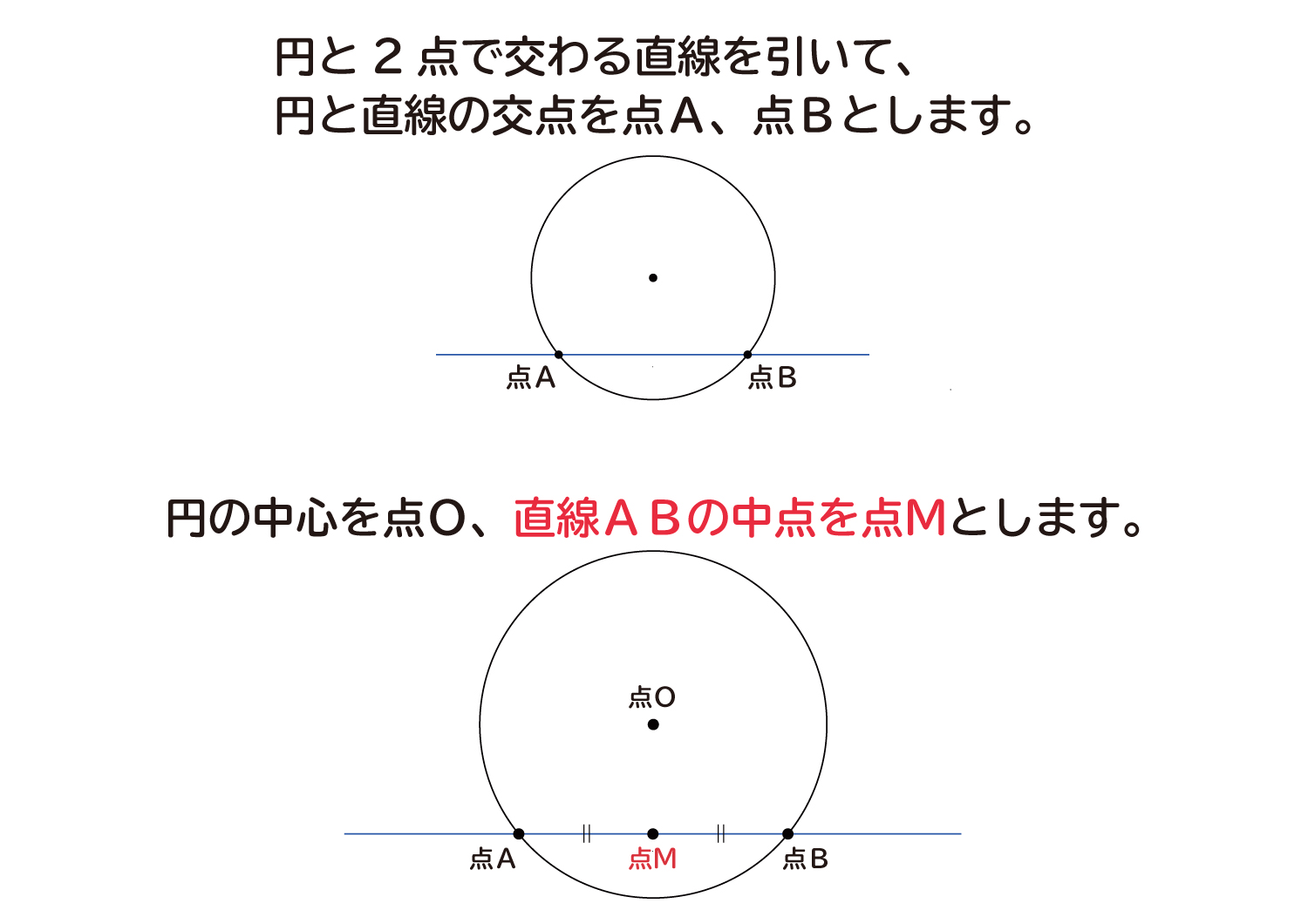
なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル

第３巻命題18 接線と半径は垂直 Stoixeia ストイケイア

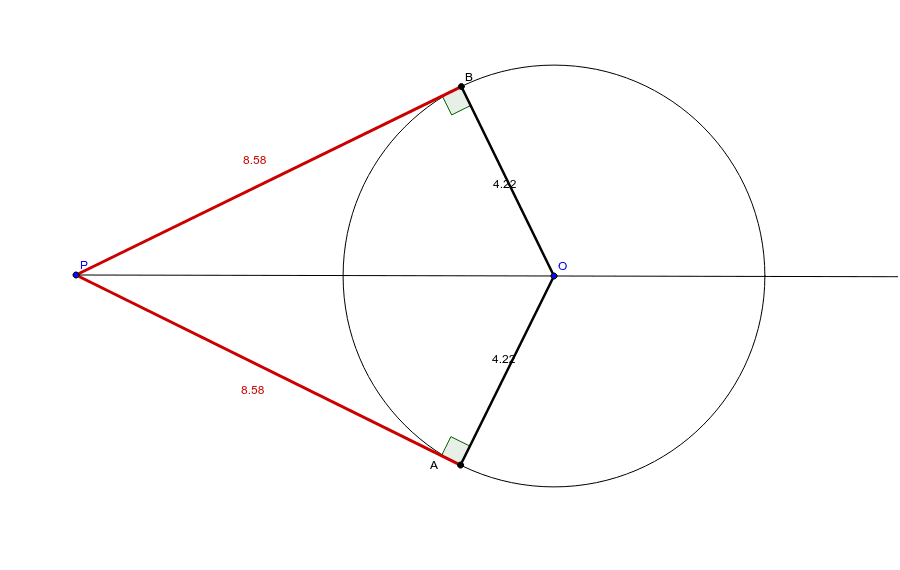
円の接線 接線の長さ Geogebra

方べきの定理とは 証明や逆 応用問題をわかりやすく解説 受験辞典

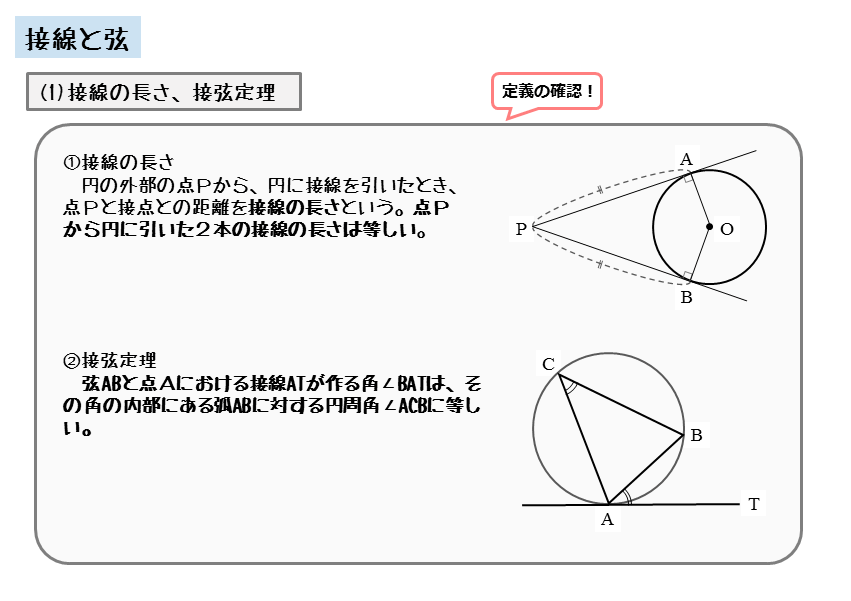
図形の性質 接線と弦について 日々是鍛錬 ひびこれたんれん

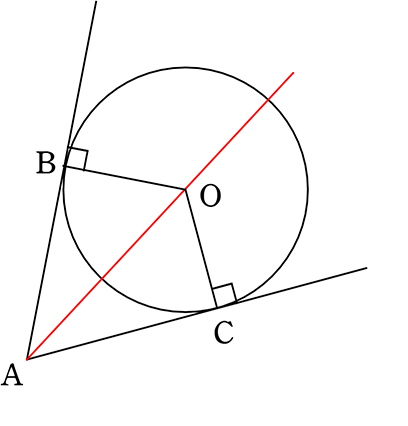
中学数学 円周角 中心角

2

高校数学a 2つの円の共通外接線と共通内接線の長さ 受験の月

円の方程式の公式や求め方をわかりやすく解説 円の接線も 受験辞典

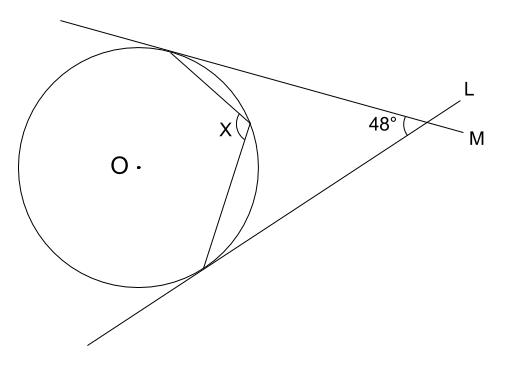
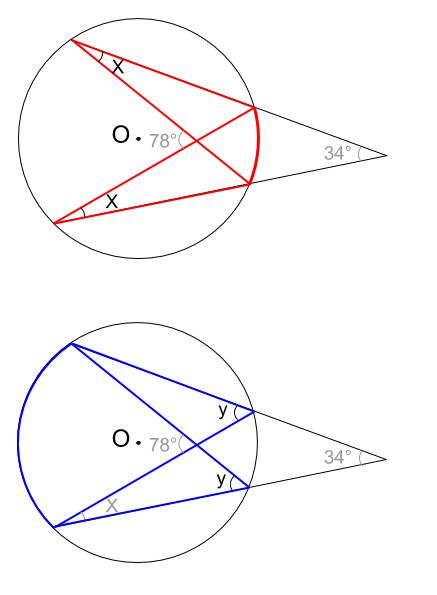
中学数学 円周角の定理 例題その４ 中学数学の無料オンライン学習サイトchu Su

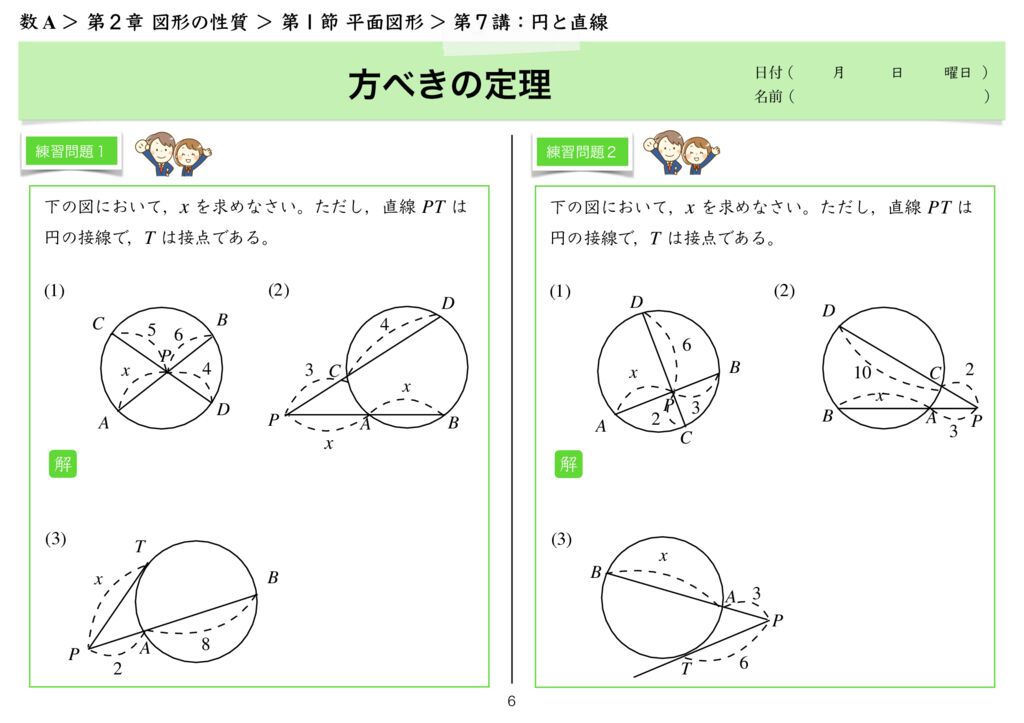
7講 円と直線 1節 平面図形 問題集 2章 図形の性質

接弦定理の証明 円周角が直角ver 数学a By となりがトトロ マナペディア

中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく

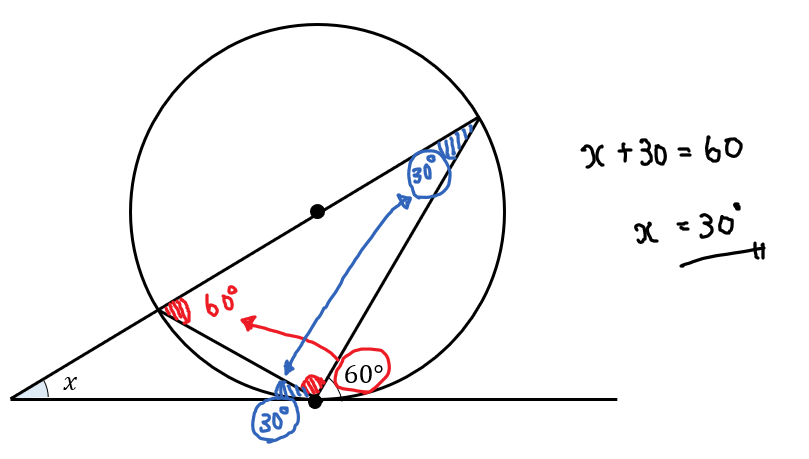
接線と弦のつくる角の定理 問題の解き方 証明をサクッと解説 数スタ

高校数学 円の接線公式 映像授業のtry It トライイット

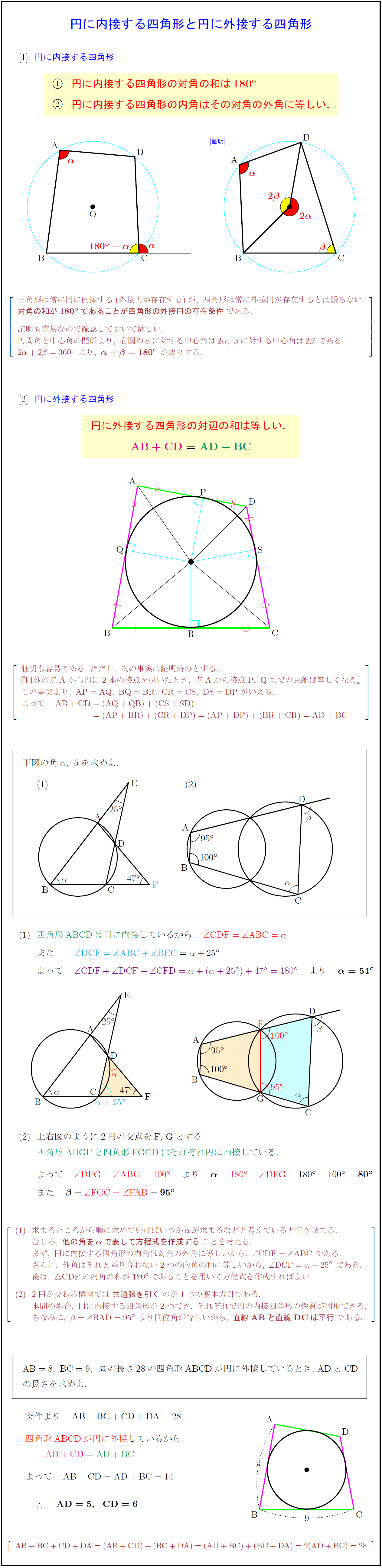
高校数学a 円に内接する四角形と円に外接する四角形の性質の証明 受験の月

原田 浩明 Pa Twitter Sサクシード059 円の接線の長さ 接弦定理 接線と弦の作る角の定理 高校 数学 １年 数学a 図形の性質 定理の証明 T Co I1zkawby6b Twitter

数学a 平面図形 円の性質 円の接線

中学３年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生

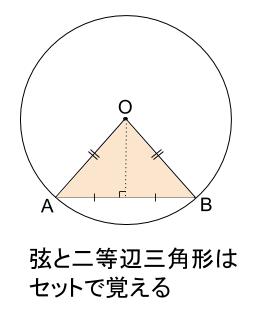
中学数学 三平方の定理 円と接線 弦 中学数学の無料オンライン学習サイトchu Su

2

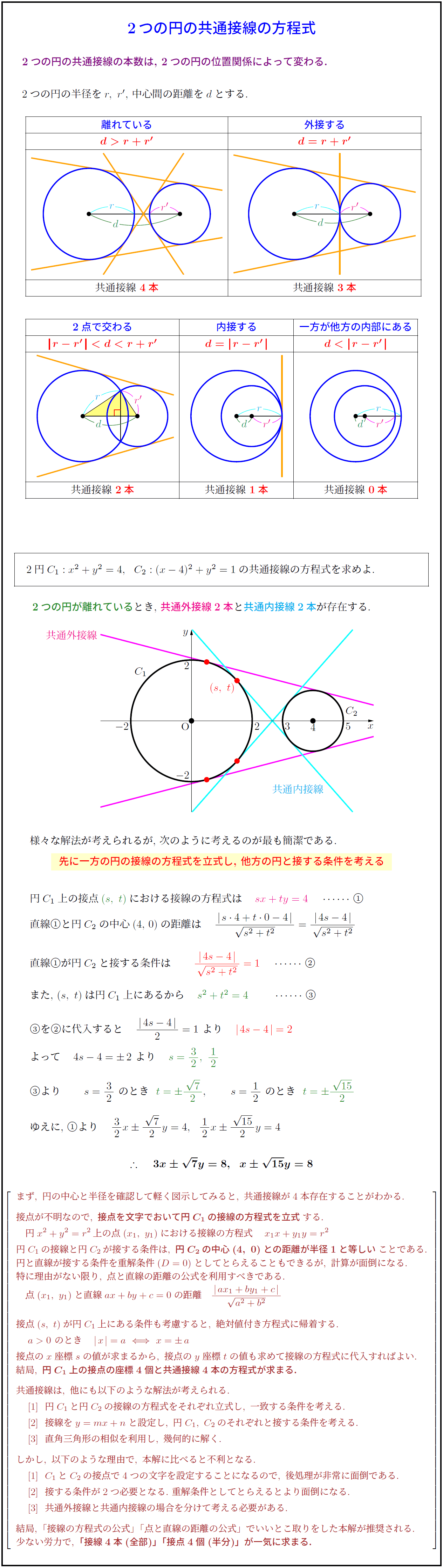
高校数学 2つの円の共通接線の方程式 受験の月

中学数学 円周角の定理 例題その４ 中学数学の無料オンライン学習サイトchu Su

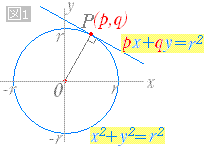
円の接線の方程式

接線と弦のつくる角の定理 問題の解き方 証明をサクッと解説 数スタ

円の接線 その基本的な性質 番外編 身勝手な主張

接弦定理まとめ 証明 逆の証明 理系ラボ

高校数学a 図形の性質 内接円と接線まとめと問題

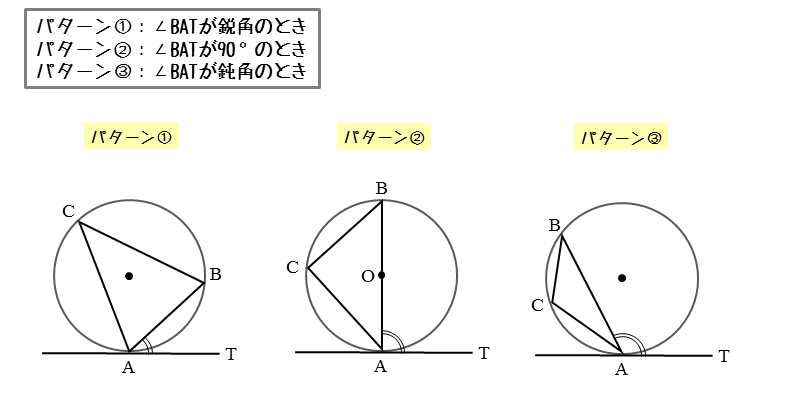
図形の性質 接線と弦について 日々是鍛錬 ひびこれたんれん

高校数学a 共通接線の長さを求める問題 例題編 映像授業のtry It トライイット

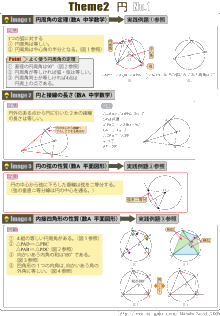
円 に関するチャートを作ってみました 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc

7講 円と直線 1節 平面図形 問題集 2章 図形の性質

接線と円と合同の証明問題 数学の要点まとめ 練習問題一覧

2

接弦定理とは何か 角度別に分かるその証明方法 アタリマエ

接線と円と合同の証明問題 数学の要点まとめ 練習問題一覧

数学a 平面図形 円にまつまる問題チャート まとめ集 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru

接線と弦の作る角 接弦定理 無料で使える中学学習プリント

連質本当に本当にsorryでございます １枚目 １ 合ってますか Clearnote

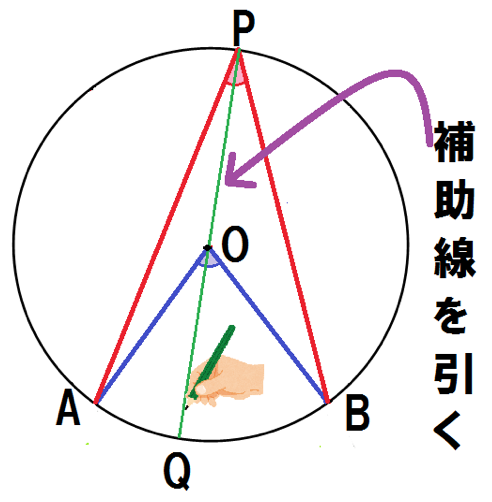
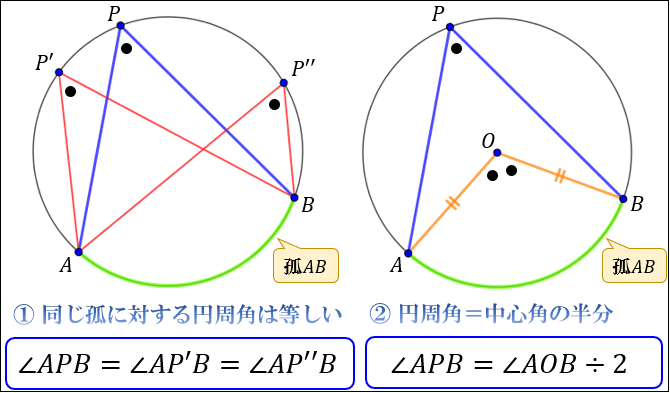
これでスッキリ 円周角の定理の証明の3つのパターン Qikeru 学びを楽しくわかりやすく

2

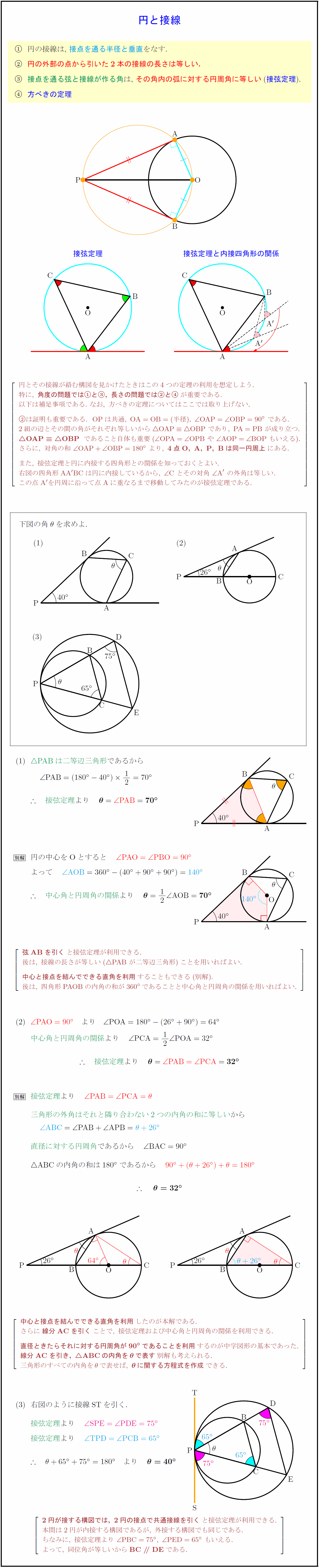
高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月

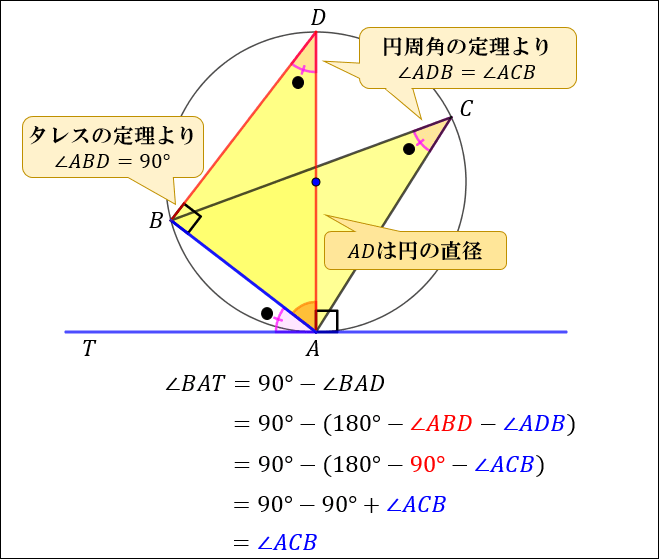
接弦定理とは何か 角度別に分かるその証明方法 アタリマエ

1

方べきの定理の証明と例題 思考力を鍛える数学

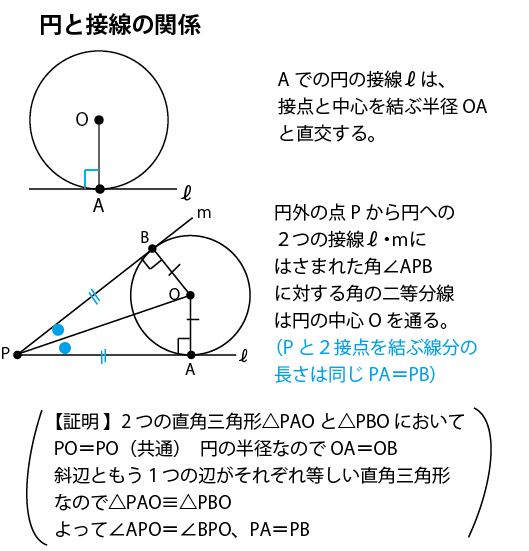
17年前期 千葉県公立高校入試数学 第2問 5 作図 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

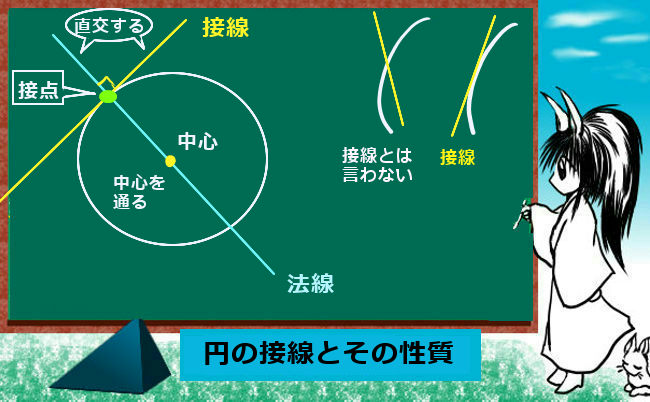
円の接線と内接 外接 理数系学習サイト Kori

図形の性質がわかません 図の Oebが90度になる理由がわかりません Okwave

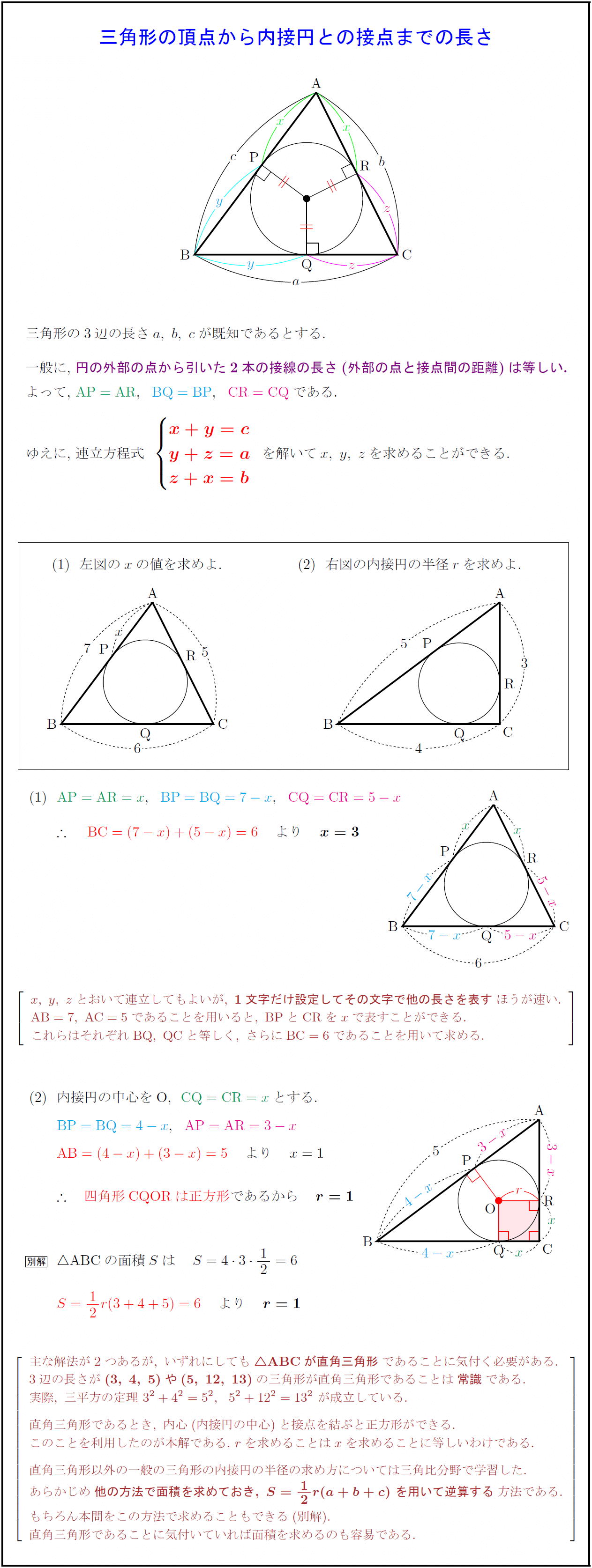
高校数学a 三角形の頂点から内接円との接点までの長さ 受験の月

数学ａの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア

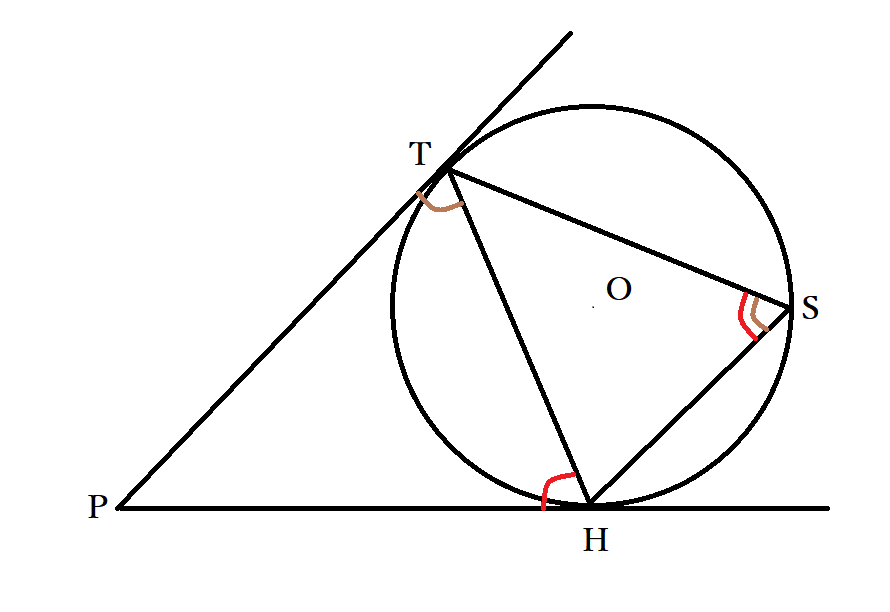
円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの学びblog

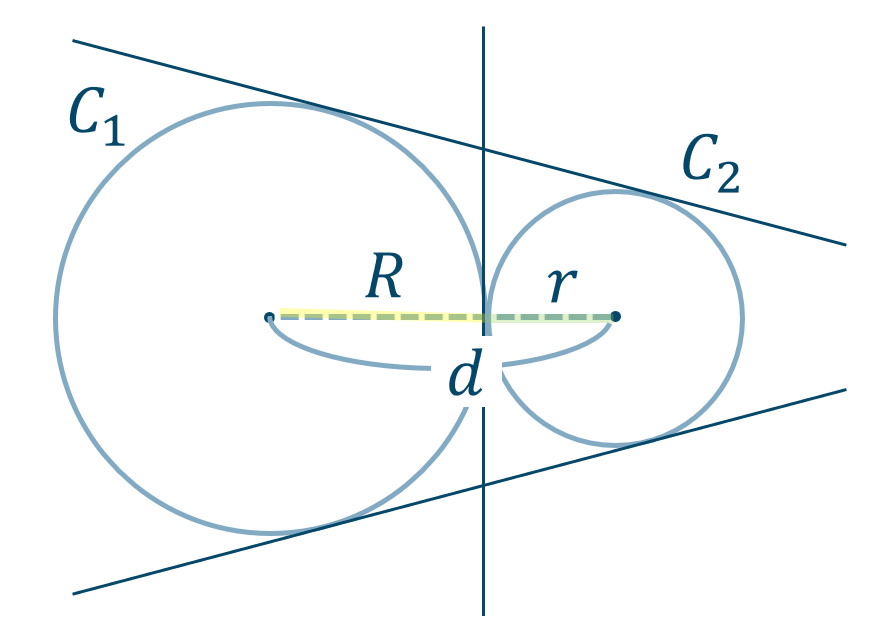
公式一覧と使い方 解き方 数学ａ 図形の性質 教科書より詳しい高校数学

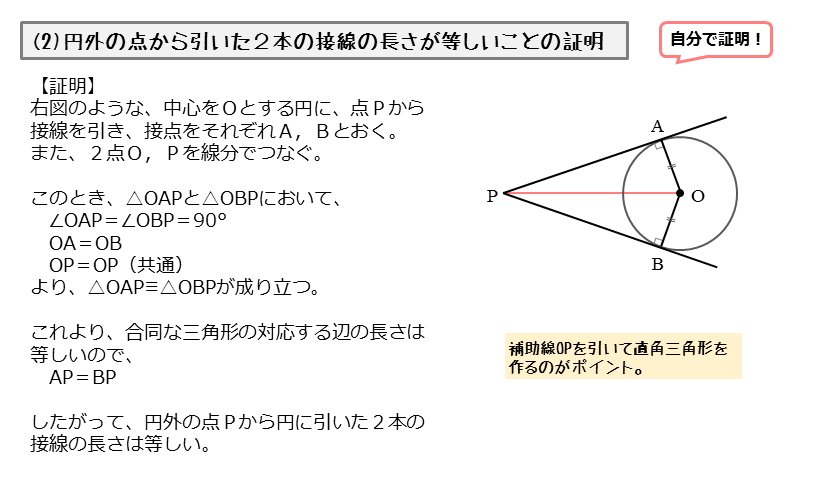
図形の性質 接線と弦について 日々是鍛錬 ひびこれたんれん

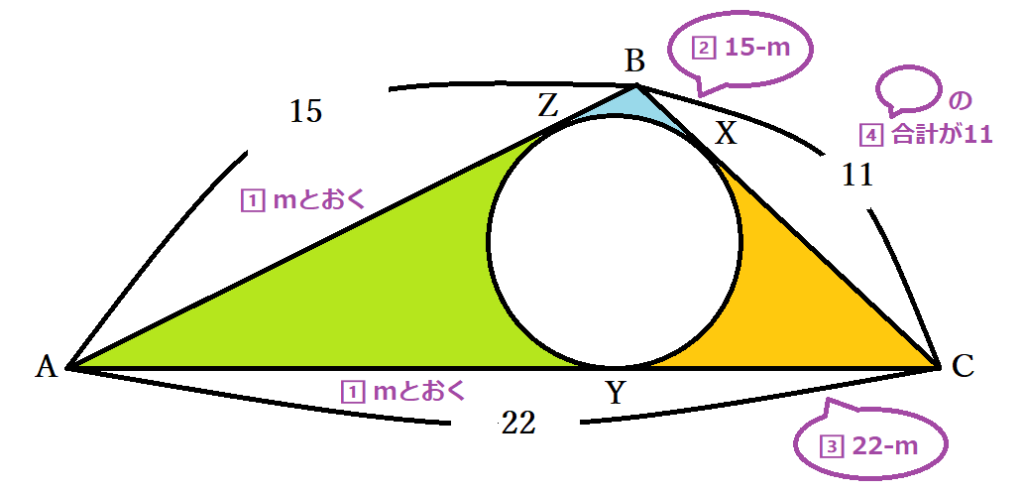
円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの学びblog

証明 円の接線は接点を通る半径に垂直である

三平方の定理の証明 方べきの定理を利用した２種類の証明をわかりやすく解説 Fukusukeの数学めも

Incoming Term: 円の接線の性質 証明,